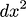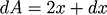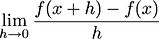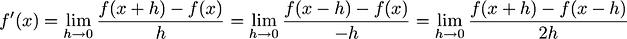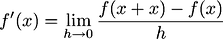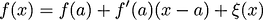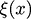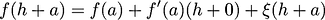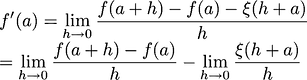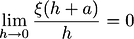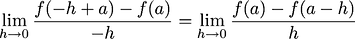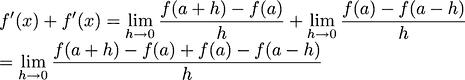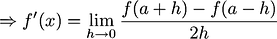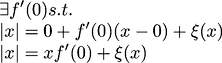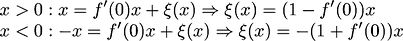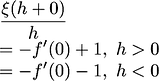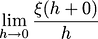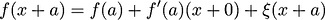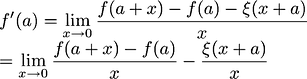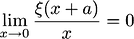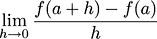neptune
Member
Hello everyone,
The derivative of function
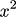 is
is
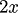 , what i understood is if function
, what i understood is if function
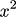 represents the graph of time and displacement, its derivative at a point on graph tells me the instantaneous velocity.
represents the graph of time and displacement, its derivative at a point on graph tells me the instantaneous velocity.
Question 1: since we find derivative by making the
 as small as we can lim->0 but we never make it a point, so why do we call it derivative at a point ? or instantaneous velocity at a point. it better be called velocity as x approaches at that particular point.
as small as we can lim->0 but we never make it a point, so why do we call it derivative at a point ? or instantaneous velocity at a point. it better be called velocity as x approaches at that particular point.
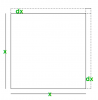
If
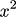 represents the area of square its derivative
represents the area of square its derivative
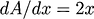 represents change in area when side is changed by small amount. but when i put in numbers in
represents change in area when side is changed by small amount. but when i put in numbers in
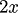 it just tells me the area at that particular point.
it just tells me the area at that particular point.
Question 2: if it tells me the area of square at particular point where is the notion of change coming in ?
and it is not accurate as it ignores the
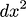 part, i could have found out the area of square much more accurately by simply putting the value in the function.
part, i could have found out the area of square much more accurately by simply putting the value in the function.
The derivative of function
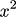
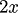
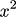
Question 1: since we find derivative by making the

If
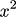
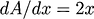
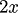
Question 2: if it tells me the area of square at particular point where is the notion of change coming in ?
and it is not accurate as it ignores the