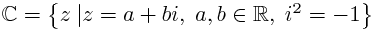why don't imaginary numbers make so much sense?

[PG1995]

PG1995,



Yes, already explained in post #3 of this thread.



It is wrong to think of operator j as a constant. Sometimes folks use j as an abreviation for 1/_90°, which is a constant. In that case, it is not being used as a operator anymore. You have to judge which is which by the context of the usage. So when used as a operator, j has no value. Neither do the other math operations ±,*,/,√,etc.

Ratch

Thank you, Ratch.

Okay, so 7j means to rotate 7 by 90 degrees CCW. When we rotate 7 by 180 degrees CCW, which as you say is shown by 7j^2 or 7i^2, we get 'real' result of "-7" but what do we get by '7j'?

I don't understand why you are saying that it is wrong to think "j" or "i" as a constant. As a side note, I personally don't consider sqrt(-1) even a constant because it evaluates to nothing and it's just a piece of 'nonsense'. The operator "j", as you describe it, comes into existence when we try to perform square root operation on -1 which is mathematically impossible.

Please help me out of this confusion. Thank you.

Regards
PG

 

[Ratchit]

PG1995,

...but what do we get by '7j'

You get a number that is 7 units long in an orthogonal relationship to a real number.

I don't understand why you are saying that it is wrong to think "j" or "i" as a constant.

Because it is defined to be a operator, even if you get correct answers treating it like a constant. Its conceptional basis is to rotate a number 90° CCW.

I personally don't consider sqrt(-1) even a constant because it evaluates to nothing and it's just a piece of 'nonsense'.

You should read my past postings. I already showed that √-1 was 1/90° in polar form. How can you say that it is nothing or nonsense? It is a number 1 unit in length orthogonal to a defined real number.

The operator "j", as you describe it, comes into existence when we try to perform square root operation on -1 which is mathematically impossible.

No, it is not. √-1 is a computable unique number. It appears you have not read or assimulated my past posts.

Please help me out of this confusion.

Read my previous posts. Do not gloss over them. Tell me specifically which post you do not understand. It does no good for me to repeat over and over again what I already posted.

Ratch

 

[MrAl]

Hello again PG,

You appear to be not reading everyone's posts in their entirety. If you go back and read post 20, you'll get more insight into what sqrt(-1) means.

The variable j is sometimes said to be a constant and sometimes said to be a variable and sometimes other. It depends on the context.

 

[PG1995]

Thank you, Ratch, MrAl.

I'm extremely sorry if you guys feel that I didn't read the previous posts carefully. Perhaps, I didn't. I offer my apologies. I would re-read the previous postings meticulously before asking any follow-on queries.

Best wishes
PG

 

[misterT]

Because it (j) is defined to be a operator, even if you get correct answers treating it like a constant. Its conceptional basis is to rotate a number 90° CCW.

It is not defined to be an operator. i is the imaginary unit. The operator concept is just a teaching method to help some people understand complex numbers more easily.

 

[ericgibbs]

Thank you, Ratch, MrAl.

I'm extremely sorry if you guys feel that I didn't read the previous posts carefully. Perhaps, I didn't. I offer my apologies. I would re-read the previous postings meticulously before asking any follow-on queries.

Best wishes
PG

hi,
For a little 'off line' study look here.

**broken link removed**

and also the attached pdf.

Googling for j operator will also bring up lots of links

 

[Ratchit]

misterT,

It is not defined to be an operator. i is the imaginary unit. The operator concept is just a teaching method to help some people understand complex numbers more easily.

If you make such a outrageous statement as the first sentence above, then you are obligated to explain why so much literature, such as that referenced by ericgibbs above, does in fact refer to j as an operator.

Ratch

 

[misterT]

If you make such a outrageous statement as the first sentence above, then you are obligated to explain why so much literature, such as that referenced by ericgibbs above, does in fact refer to j as an operator.

Because they teach the concept of thinking j as an operator. Nothing wrong with that. But they do not say that it is the definition of i.. or if they do it is only in electrical engineering context when the j symbol is used.

 

[Ratchit]

misterT

The texts say it is an rotational operator. You can't get more defining than that. Certainly it does not mean a constant.

Ratch

 

[misterT]

The texts say it is an rotational operator. You can't get more defining than that. Certainly it does not mean a constant.

There are at least equally many texts saying otherwise. The ones teaching the operator thing are wrong. Ok teaching method though.. (We can continue this as long as the thread is closed.)

 

[KeepItSimpleStupid]

Mmmm! I just got a new book and coincidentally it has an interesting equation in it:

|Z-w|=r or |z-w|^2 = r^2 or

and

|z-w|^2 = (z-w) * (z-w)^* =

(x-u)^2 + (y-v)^2 = r^2

Without the pic, it says that (u and v) are the co-ordinates of the circle center in the complex-z plane and r is the radius.

The notation of (z-w)^* ; I'm using ^* to denote a superscript and I would imagine that it's a complex conjugate.

So, we have equations of circles in the complex plane. Not something that I have seen before.

A real x and a real y with a complex z is easily seen, but can you have a real x, y and z and a complex z plane?

Most of the z are italicized except the one in bold.

 

[Ratchit]

misterT,

There are at least equally many texts saying otherwise. The ones teaching the operator thing are wrong.

Its not about how many say yea vs. nay. It is the quality of of the texts. So by your algebraic way of thinking, would not jω mean the sum of j pieces, each one being ω in size? Can you wrap your mind around that? Where does orthogonality come into play with that definition? Doesn't it make more sense to say that ω is rotated 90° CCW?

Ratch

 

[MrAl]

Hi,

The imaginary operator j (also called the imaginary unit) is sometimes considered a constant probably because it is sometimes defined in a way similar to a constant. But it does not always act like a constant so to say it is *only* a constant is not correct either.

For an example of a constant, lets start with the number '3' which we all know is a constant, and use it in an equation:
y=1+2+3

and we can easily compute y to come out to be y=6, so note that our result is a constant also.
Now lets do an equation with 'j' in it:
y=1+2+j

and now we compute y, and it comes out to be y=3+j. What happened? This isnt really a constant anymore, yet we can still call it a constant if we want to because we can say it is a constant complex number.

So in case 1 we ended up with a real constant, and the second case we ended up with a complex constant, but we may want to note that in the second case we could not add j the same way we did in the first case, so there is a difference. That's why the j is usually referred to as the imaginary operator. It forces operations on the number to take a different route than with an ordinary constant like 2 or 3.

Now we usually think of things like '+', '-', as operators so it seems strange that a 'letter' could be called an operator too. But again, in elementary algebra the plus and the minus are operators and letters are variables, but as we get into more advanced math we find there are other kinds of operators that are sometimes represented by letters or symbols. In other words, we are not limited to what we can call an operator simply because we never heard this term applied to other symbols. We live and learn and that means adding to our mathematical vocabulary.

For another example of an operator that is not one of the basic +, -, etc. type, look up the
"Laplace Operator".

While you are looking into these topics involving 'j', you should also look into the complex plane. That will help give you a more well rounded education in this area.

 

[misterT]

Mmmm! I just got a new book and coincidentally it has an interesting equation in it:

|Z-w|=r or |z-w|^2 = r^2 or

and

|z-w|^2 = (z-w) * (z-w)^* =

(x-u)^2 + (y-v)^2 = r^2

Without the pic, it says that (u and v) are the co-ordinates of the circle center in the complex-z plane and r is the radius.

The notation of (z-w)^* ; I'm using ^* to denote a superscript and I would imagine that it's a complex conjugate.

So, we have equations of circles in the complex plane. Not something that I have seen before.

A real x and a real y with a complex z is easily seen, but can you have a real x, y and z and a complex z plane?

Most of the z are italicized except the one in bold.

This is how I figured that out:

|z-w|=r

Here z and w are complex numbers, so |z-w| is the distance between them. If this distance is constant r we have a circle.
(r must be real number if it is the distance between two complex numbers.)

Then the equation is raised to the second power. This is done to get rid of the modulus (or the absolute value, or magnitude) operation. It looks strange because there are two complex numbers, but if we first define a complex number c = z-w, we get more nicer form of the next identity:
|c|^2 = cc*

This (above) is the same as yours: |z-w|^2 = (z-w) * (z-w)^*

Finally it is assumed, or more precisely, z and w are defined to be the:
z = x + yi
w = u + vi
and therefore:
c = (x-u) + (y-v)i

(i is the famous imaginary unit. x, y, u and v are real)

and because cc* = Re(c)^2 + Im(c)^2 =
(x-u)^2 + (y-v)^2 = r^2

Work out the calculation of cc* by hand and it will come clear to you. Also notice that in the original equation |z-w|=r we have only real numbers, because |z-w| is a real number. So that is why the result:
(x-u)^2 + (y-v)^2 = r^2
is purely real.

If you look at the result carefully, you will see that the complex number w fixes the center of the circle, and r fixes the radius. Assuming z is a variable and w and r are constants.

 

[misterT]

For another example of an operator that is not one of the basic +, -, etc. type, look up the "Laplace Operator".

I hope you are not mistaking the parameter s (which is just a complex number) in Laplace transforms for a Laplace Operator Δ.

 

[misterT]

Its not about how many say yea vs. nay. It is the quality of of the texts. So by your algebraic way of thinking, would not jω mean the sum of j pieces, each one being ω in size? Can you wrap your mind around that? Where does orthogonality come into play with that definition? Doesn't it make more sense to say that ω is rotated 90° CCW?

It makes more sense to say that j is multiplied by ω.. resulting the point (0,ω) on the complex plane. Imaginary axis is orthogonal to real axis and j is purely imaginary (and unit length).

Calling j an operator is purely an electrical engineering thing. And that is how it is introduced in every electrical engineering book. It is very powerful way to describe dynamic signals. Maybe that's why electrical engineers don't want to call it a constant.. Because they relate it so strongly to dynamic systems (and phasors).

Here is a strictly mathematical definition of complex numbers:

[LATEX]\mathbb{C} = \left \{ z \: | z=a+bi,\; a,b \in \mathbb{R},\; i^{2}=-1 \right \}
[/LATEX]
The imaginary unit i is equal to the point (0,1) on the complex plane.
https://mathworld.wolfram.com/ImaginaryUnit.html
https://mathworld.wolfram.com/ImaginaryNumber.html
https://mathworld.wolfram.com/ComplexNumber.html
**broken link removed**
https://en.wikipedia.org/wiki/Imaginary_unit

So, I let you call j as an operator (in the context of electrical engineering). But don't (Ratchit) tell me (or anybody else) that: "The symbol 'i' does not mean √-1. 'i' is a mathematical operator, not a finite value."

 

[Ratchit]

misterT,

It makes more sense to say that j is multiplied by ω..

OK, so you are more comfortable with ωj, the sum of ω pieces, each on being j in size? What does that mean?

resulting the point (0,ω) on the complex plane. Imaginary axis is orthogonal to real axis and j is purely imaginary (and unit length).

What gives you the basis for saying j is orthogonal if you reject it as being a rotational operator?

Calling j an operator is purely an electrical engineering thing.

It only seems that way because EE is where one often runs into multiple phases.

And that is how it is introduced in every electrical engineering book.

No, sometimes they treat it like a constant. Like most of the linked references you gave.

It is very powerful way to describe dynamic signals.

Every signal is dynamic. If it was not dynamic, it would not be a signal. It is a good way to represent orthoganality in any entity, not just signals.

Maybe that's why electrical engineers don't want to call it a constant.. Because they relate it so strongly to dynamic systems (and phasors).

What has that got to do with anything? They want to call it an operator because that is what it is.

Here is a strictly mathematical definition of complex numbers:

Those are not definitions. They are symbolic representations.

The imaginary unit i is equal to the point (0,1) on the complex plane.
https://mathworld.wolfram.com/ImaginaryUnit.html
https://mathworld.wolfram.com/ImaginaryNumber.html
https://mathworld.wolfram.com/ComplexNumber.html
Euler's Investigations on the Roots of Equations
https://en.wikipedia.org/wiki/Imaginary_unit

All the references to Wolfram and Wikipedia assume j is a constant. The Euler reference has nothing to do with what we are talking about. None of the references show why j is a constant. They treat it like a constant and get correct answers. But we have been through that before. None of the references prove it is a constant and disprove it as being a operator. You have still not elucidated us on what jω or ωj means from a algebraic point of view.

So, I let you call j as an operator (in the context of electrical engineering). But don't (Ratchit) tell me (or anybody else) that: "The symbol 'i' does not mean √-1. 'i' is a mathematical operator, not a finite value."

The j-operator in the context of electrical engineering has no different meaning. It is what it is regardless of how or where it is used, provided it is used correctly. I said before that sometimes folks use plain j instead of 1j to mean 1 rotated by 90°. In that context, j is a constant. But used as jω, j is a rotational operator, pure and simple.

Ratch

 

[MrAl]

I hope you are not mistaking the parameter s (which is just a complex number) in Laplace transforms for a Laplace Operator Δ.

Hi there misterT,


Your hopes have come true, i am not mistaking anything

Also, i have no problem stating that X1=2+3j is a constant complex number, while X=a+bj is a variable complex number.
Some of the nomenclature depends on the context so we'll find references for j saying both "operator" and "constant".
j is an operator because of the way it works, but j can be a constant because it's value does not change like a general variable like x.
j is always equal to sqrt(-1) so it can be called a constant, yet it has more meaning than that so restricting it to that isnt right either.
Geometrically it's more of an operator, but algebraically it's more of a constant.

 

[misterT]

All the references to Wolfram and Wikipedia assume j is a constant. The Euler reference has nothing to do with what we are talking about. None of the references show why j is a constant. They treat it like a constant and get correct answers. But we have been through that before. None of the references prove it is a constant and disprove it as being a operator. You have still not elucidated us on what jω or ωj means from a algebraic point of view.

All the references show you that i is defined to be √-1 and it has a finite value. When i is defined to be √-1, it proves that it is not defined as an operator. Stop being stupid on purpose.

The proof in algebraic point of view is in number theory, complex numbers form a field. In history there was attempts to form complex numbers with two imaginary units, but they couldn't make it work as a number system. Then one day sir William Hamilton discovered that three dimensional complex numbers (three imaginary units, all orthogonal to each other) did work as a number system (field).. they are called "Quaternions". If j would be defined as an operator, it would work in all dimensions, but it doesn't.

https://mathworld.wolfram.com/Field.html
https://mathworld.wolfram.com/Quaternion.html

Other proof from algebraic point of view comes from the way multiplication of complex numbers is defined: (a+bi)(c+di) = (ac-bd) + (ad+bc)i
if c = 0 and d = 1, the other complex number becomes purely imaginary and unit length and the multiplication becomes: (a+bi)(0+1i) = (a0-b1) + (a1+b0)i = -b + ai
And we see that the coordinate point of the first complex number is rotated by 90 degrees. This happens because the way multiplication is defined, the value of the complex numbers and because by definition i = √-1. Not because "i is defined as rotational operator".

And here is a translation of Eulers work:
https://www.electro-tech-online.com/custompdfs/2011/09/Euler_170_Doucet.pdf

Show me some proofs and references to back up your opinions for a change. It is easy to say ignorant, meaningless, things like:
"Those are not definitions. They are symbolic representations."
"They want to call it an operator because that is what it is."
"Every signal is dynamic. If it was not dynamic, it would not be a signal."
"It is what it is regardless of how or where it is used"
"The symbol 'i' does not mean √-1. 'i' is a mathematical operator, not a finite value."

 

[Ratchit]

misterT,

All the references show you that i is defined to be √-1 and it has a finite value. Especially the Euler reference shows you the algebraic point (notice there are 4 pages of it, you can change the page from upper right corner). When i is defined to be √-1, it proves that it is not defined as an operator. Stop being stupid on purpose.

All that proves is that correct answers can be obtains by assuming j=√-1 because of its conformal similarity. That does not prove j is a constant or that it is not a rotational operator. My apologies for not noticing more pages for Euler.

The proof in algebraic point of view is in number theory, complex numbers form a field.

A field is a spacial distribution of a quantity. Numbers can be represented as coordinates within a field, but that in itself is not a proof of their orthogonality.

In history there was attempts to form complex numbers with two imaginary units, but they couldn't make it work as a number system. Then one day sir William Hamilton discovered that three dimensional complex numbers (three imaginary units, all orthogonal to each other) did work as a number system (field).. they are called "Quaternions". If j would be defined as an operator, it would work in all dimensions, but it doesn't.

How does that explain what jω or ωj means?

Other proof from algebraic point of view comes from the way multiplication of complex numbers is defined: (a+bi)(c+di) = (ac-bd) + (ad+bc)i
if c = 0 and d = 1, the other complex number becomes purely imaginary and unit length and the multiplication becomes: (a+bi)(0+1i) = (a0-b1) + (a1+b0)i = -b + ai
And we see that the coordinate point of the first complex number is rotated by 90 degrees. This happens because the way multiplication is defined, the value of the complex numbers and because by definition i = √-1. Not because "i is defined as rotational operator".

Again we see that a correct answer was found by treating i as √-1. But what gave the basis of A+iB to be A + B/_90° in the first place? It was j being defined as a rotational operator.

Ratch