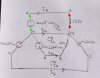
Hello again,
Well, dont worry too much about the source type, delta or wye, when considering the circuit with no neural wire.
The reason for the higher currents could be because the differential voltage is higher: 208vac line to line as opposed to 120vac line to neutral.
But to make a better assessment i think we need to consider different kinds of loads, including a fully 'balanced' load. To find out for sure, do another problem with a balanced load and compare. Note that the wye source voltage neutral is zero volts and so is the balanced load 'fake' neutral.
Well, dont worry too much about the source type, delta or wye, when considering the circuit with no neural wire.
The reason for the higher currents could be because the differential voltage is higher: 208vac line to line as opposed to 120vac line to neutral.
But to make a better assessment i think we need to consider different kinds of loads, including a fully 'balanced' load. To find out for sure, do another problem with a balanced load and compare. Note that the wye source voltage neutral is zero volts and so is the balanced load 'fake' neutral.