'r-e-s-i-s-t-o-r'
New Member
Hello friends!
Me and my friend are working on a project in school, in which we are intending to record sound using a michrophone, filter out unwanted frequencies using a band pass filter circuit (see: below), and finally send it out through a speaker.
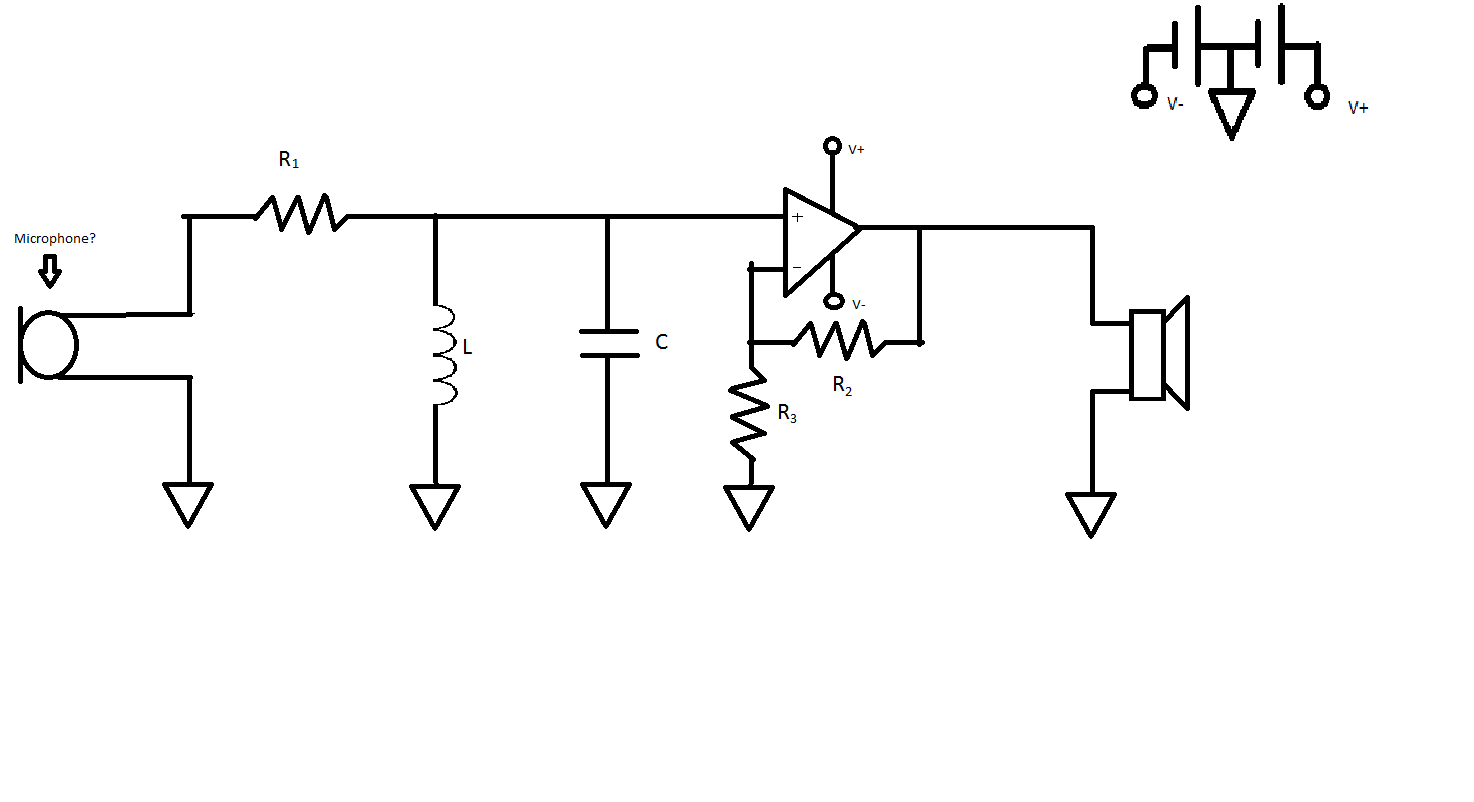
Lowest frequency= (R1)/(2πL)
Highest frequency= 1/( 2π(R1)*C )
Gain= 1+R2/R3
π=pi
We're planning on using a very small microphone, and a very small speaker.
Do you think this circuit will work the way we want it to? We've got very little knowledge in electronics, the circuit and formulas are based on things we found online.
Me and my friend are working on a project in school, in which we are intending to record sound using a michrophone, filter out unwanted frequencies using a band pass filter circuit (see: below), and finally send it out through a speaker.
Lowest frequency= (R1)/(2πL)
Highest frequency= 1/( 2π(R1)*C )
Gain= 1+R2/R3
π=pi
We're planning on using a very small microphone, and a very small speaker.
Do you think this circuit will work the way we want it to? We've got very little knowledge in electronics, the circuit and formulas are based on things we found online.
