second order differential equations & Laplace

[derick007]

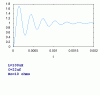
Hi all, this is my first post so please bear with me - any advice/support would be warmly welcomed. I have been doing some work on a simple RLC electronic circuit whose transfer function follows the standard second order transfer function.
The forcing function (input) is a periodic square wave function and I am trying to write an equation for the output - time based.

Please find 2 documents attached in which I have tried to develop equations for the output using 2 different methods. The first one is using complementary function and particular integrals (which I do not like). The second one uses Laplace transforms. I have found a time based equation but when i input times i do not think i am getting the correct output values. Can someone please have a look -
particularly the Laplace pdf.

Many thanks, derek
Could not upload the file as internet explorer could not find page

 

[MrAl]

Hi,

Yeah we can not see the work you have already done so maybe try uploading again or else upload to another site and link here.

Laplace can make things simpler that's for sure.

 

[derick007]

View attachment LAPLACE.pdf

 

[MrAl]

Hi again,


You should also show your circuit. An RLC circuit can be in many different configurations. You probably mean the following:
1. The forcing function is a voltage source that is a square wave.
2. The RLC circuit is a series circuit.

So we have a square wave voltage exciting a series RLC circuit.

But what else remains to be known is where you are taking the output from. It is across the cap, resistor, inductor, or across a pair like cap and inductor, etc. Or are you taking the output to be the current through the network.

So you'll have to verify or correct this information and also state where you want to take the output from. A drawn circuit would be best but you can describe it if you like as long as you are very specific about what the circuit looks like and where the output is taken from.

Also, what time period of the response do you want to solve for. Just the first period or several cycles down the road or the final solution (near t=infinity) which may mean you want the average value after a long time has passed since the circuit was turned on.

What we also have to know is the clear description of the input wave. It's a square wave, but that's not really enough information. We also need to know the amplitude and offset if any. From your drawing it looks like maybe 1 unit high and the bottom is at 0, but you might want to clear this up too because square waves also commonly run plus and minus 1 unit and are centered at zero amplitude.

If you could state the component values too that would be nice. I think you want 10 ohms for the resistor?

 

[derick007]

Thank you Mral for your time and patience. Hopefully the attached document will answer all of your questions. The document is my attempt to solve exactly the same RLC circuit but uses the complementary function and particular integral.

C = 22uF, L = 100uH, Ro = 10 ohms (can be 1, 10, 100 etc.)
Forcing input function is a square wave with zero offset and does not go negative, freq. = 43Khz, amplitude = 23.5v, T=23.25us, duty cycle = 0.28 Ton = 6.43us Toff=16.8us


Kind regards, derick007

 

[MrAl]

Hi again,


Just to check, you know that the transfer function of the circuit is not what you wrote in that original paper you posted right? Not sure if you were doing another circuit or this more recent one. Might want to double check that. The transfer function for this more recent circuit is:
Vo(s)/Vi(s)=Ro/(Ro*s^2*C*L+s*(C*Ro*RL+L)+Ro+RL)

To start with you'll need that for the first paper method unless that was a different circuit?

Also, it looks like you are correct about using the Delay and Periodic operations in the first paper. The delayed negative pulse 'turns off' the first pulse thereby creating a square wave. The denominator sets the periodic time period as you did.

And what value is RL ?

 

[derick007]

Hi MrAl, thanks again for getting back.
Apologies again. RL is the equivalent resistance of the inductor which I have assumed to be negligible i.e. RL=0.
Putting this into the equations you should find the transfer functions for both papers are the same.
I am really glad you agree with my method, however i have used the inverse laplace transform to find a time based equation for the output, when the input square wave forcing function has an amplitude of 1v. Please see attached spreadsheet. The time intervals i have used is 1us, but the output the equation generates is not what i expected. I expected the output to rise exponentially from 0v, however the equations state the output starts at 1v or 23.5v if the input waveform had an amplitude of 23.5v????

 

[derick007]

View attachment Copy of mc34063A (2).pdfoops

 

[derick007]

View attachment Copy of mc34063A (2).pdf

 

[MrAl]

Hello again,


Ok we both have the same transfer function now, thanks for clearing that up. So then we are making RL=0 for now.

You're right in that the response will not start out high, but will start out at zero, then rise up expo-sinusoidally (a damped sinusoidal) with equation:
Vout(t)=1+e^(-at)*(A*sin(wt)+B*cos(wt))
where A and B are negative.
So you can see that when t=0 the sin part goes to zero and the cos part goes to -1, so the result is Vout=1+0-1=0.

That's for a step response, which i have to recommend to you to perform the calculation for first before doing the square wave input. Do a simple step wave first (unit step) and see if you can match those results. The output with a unit step input should look like the attachment.

 

[derick007]

Hi MrAl

I already have found the step response as per the attachments below. Apologies for the quality of the attachments. I have one spreadsheet with many worksheets containing many tables calculating values and then plotting these on a graph. I open each of these worksheets and save them as a pdf which I can attach to posts. As you probably know the inverse Laplace transform of a unit step response of a standard second order system is published widely - i just used this time equation and inserted my component values to get the responses. I noted the value of the resistance (load resistance) had a significant effect on the damping.

However, I will plot the step respose from the equation i have produced to see what effect it has.

View attachment Copy of mc34063A (2).pdf

View attachment Copy of mc34063A (3).pdf

 

[MrAl]

Hi,


Yeah that equation just is not correct, sorry to say. You'll have to try again. The sin and cos terms are always separate terms there is never a cos term inside a sin term like this: sin(cos(x)).

The correct form again is like this:
Vout(t)=1+e^(-at)*(A*sin(wt)+B*cos(wt))

where A and B are both negative, or alternately we can write it as:

Vout(t)=1-[e^(-at)*(A*sin(wt)+B*cos(wt))]

and then A and B are both positive, but notice the only thing inside the sin() and cos() brackets is "wt", there's never a cos(anything) inside there.

So something is seriously wrong. You should try to get this unit step response right first then go from there. It could be that you just wrote it out wrong during copying or something so maybe check that first.

ADDED NOTE:
I wasnt able to view your picture (second attachment) for some reason, just the first pdf file. That's where i see your equation.

 

[derick007]

Hi MrAl
I have found the step response as part of my calculations for the periodic square wave response i.e. inverse laplace transform of 1/(s(s+a)(s+b) where a and b, in my case are complex numbers. You will see in my laplace document the time equation is as you note above apart from A and B being negative (in my case A and B are +ve, very small +ve nos. and the 1 + e, in my case is 1 - e). Therefore at t=o I have

1 - 1 (very small +ve no. = 0 + 0 ) = 1 - very small +ve no. = 1 - 0 = 1.

From this I would conclude that although in my case A and B are the correct sign i.e. +ve, they are the wrong value, in fact B must =1 ?

Interested in your thoughts/opinions, kind regards, Derek

 

[derick007]

Hello again MrAl
I have looked at my calcs again and cannot find were I might be going wrong : A=2.34x10^-10 and B=2.2x10^-9 ?

I have been pulling my hair out trying to find a mistake, but cannot. Any suggestions ?

Kind regards, derek

 

[derick007]

Hi MrAl

Not much hair left now, but i think i have made some progress.

The problem may have been the way i was breaking the polynomial into partial fractions. I will let you know how i get on.

Regards, Derek

 

[MrAl]

Hi,

OH yes good idea. That's a easy place to go wrong. We can go over that if you still have a problem.

I must have missed your previous replies or something as i see they were dated a couple days ago. I've been a little more busy than usual around here, but im not sure how i missed those replies. But anyway, you're on the right track now.

 

[derick007]

Hello Mral

I have found the unit step reponse formula as you have quoted above - I can send the derivation if you wish.

However I have put the equation into a spreadsheet with various values and seems to work apart from the first 50 us, were the output appears to go slightly negative ?

Your thoughts and comments would be welcome.

In the meantime, now i think i have found the unit step response (apart from the first 50 us !!!!) i will have ago and finding the response for a periodic square wave input.


Regards, Derek

 

[derick007]

oops, apologies ss attached this time

View attachment Copy of mc34063A (2).pdf

 

[MrAl]

Hello again derick,


Well im very sorry to say this but something still isnt right. The output at the first instant of time has to be zero (0.000000) because all the voltage appears across the inductor and the initial voltage of the capacitor is zero and the initial inductor current is zero.

Again this is using the following values which we had been using in order to make comparison of our separate results easier:
L=100uH
C=22uF
R=10

You may wish to note that the response is an exponentially damped sinusoidal with R>=1.066 ohms. With R less than that we have to consider another type of response, but R=10 is a good choice for now so we'll stick with the damped sinusoidal.

Since your G(s) is correct, i can only imagine that you must be making a mistake in the transformation from G(s) to what you are calling the time function: Y(t).

Y(t)=1-e^(-at)*[A*sin(wt)+B*cos(wt)]

and you end up with A=B, but in real life we almost never end up with A=B as A is almost always different than B. It's true that they are both negative, but still they are not equal. I didnt want to yell out the result yet but just for a hint they are different by almost a factor of 10.

Also, when we do a simple circuit like this analytically, we never get results that are off by as much as 0.01 or -0.01. If they are off they would be off by a tiny amount like 1e-14 or -1e-14 on a typical PC computer using 16 digit floating point math. That's because the equations are so incredibly exact that the only error can come in during the numerical evaluation, and that's usually very accurate for small simple equations like this resulting time equation.
Just for reference, the numerical result for this problem is slightly greater than +200uv at t=1us.
You might also be interested to know that you can always check your results with a numerical simulator program like LT Spice.

Just to add an additional note, we can do this problem in a purely numerical environment (numerical calculations only) and that will back up our analytical results. This is also very interesting as im sure you will find. We can use a standard approach for ODE's to get there so it wont be a waste of time where we can only do this on this one application but can do this for many different applications too

 

[derick007]

Hi MrAl
Once again thank you for your patience and very detailed reply.

I am not entirely happy with the inverse Laplace transform and will start by having another look at this.

I do have a simulator from Labcenter Electronics - Proteus (schematic capture, simulation and pcb design software). However I only basic modules to cover simple pcb design and a simulator for a particular range of pic micros - I dont have the module for analogue simulation. I may purchase one in the future, but in many ways, having one means you really dont need to do alot of work solving maths problems and I always like to know "whats underneath the hood".

Many thanks, Derek