Mr RB
Well-Known Member
MisterT-
Excellent catch! I completely missed that and just used perms per number of cylinders.
Good, I thought that /8000000 was funky.
Another good catch! I forgot the 8bit mask, which of course includes the "held" bit. That now looks to be correct for calculating the number of states. Much appreciated.
That is correct, assuming the cache value itself is used as the RNG output with no further processes.
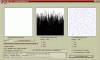
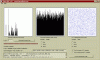
Yes and no. The testing on the cache contents has shown them to be be very high quality entropy, and the cache is used to determine the state of the cylinders and mask value (ie the overall state). So based on the entropy results we have available you can assume for statistical purposes the odds of any state occuring *approaches* that of being "equally possible" as it would with any other source of high quality entropy.
Agreed, stupidly small. So for a ball park period figure where a global repeat starts to become expected we could use (say) period / 3?
If you use 17 cylinders and the possible cylinder values are the 18 numbers: {1,2,3,1,2,3,4,5,7,1,2,3,6,4,1,3,11,9}
Number of unique cylinder permutations is:
18! / (4! * 3! * 4! * 2!) = 926 269 344 000
You must divide by the factorials because you have number 1 four times in the possible values, number 2 three times etc.
Excellent catch! I completely missed that and just used perms per number of cylinders.
You cannot include the pointer position in the calculations,
Good, I thought that /8000000 was funky.
If you have a million bit cache, you have 926 269 344 000 * 2^1000000 * 2^8 unique states. The last 2^8 comes from the exchanged bit history.
Another good catch! I forgot the 8bit mask, which of course includes the "held" bit. That now looks to be correct for calculating the number of states. Much appreciated.
And after each state the sequence of random numbers is always the same. So, if one state comes up twice, the generated numbers (states) start repeating.
That is correct, assuming the cache value itself is used as the RNG output with no further processes.
Above calculations assume that each state is equally possible and independent.
Of course, the states are not independent in the Black RNG. Black RNG defines an ordered set of states (like basically all RNG algorithms do).
Yes and no. The testing on the cache contents has shown them to be be very high quality entropy, and the cache is used to determine the state of the cylinders and mask value (ie the overall state). So based on the entropy results we have available you can assume for statistical purposes the odds of any state occuring *approaches* that of being "equally possible" as it would with any other source of high quality entropy.
The maximum period you can theoretically get is the number of unique states, but the odds of this happening is very small.
Agreed, stupidly small. So for a ball park period figure where a global repeat starts to become expected we could use (say) period / 3?