Mr RB's RNG and RNGs in general

[misterT]

I just finished implementing the Black RNG. I used a cache of 3.2 million bits and iterated the cache 100 times with an engine recommended by Mr Black (10 cylinders + 1 hold).

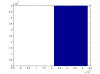
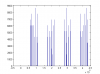
Attached is a histogram of the 100 000 x 32bit unsigned integers that was generated. Does not look too good for me. The smallest number generated was 11936.. above that the distribution looks quite even. But, I think I'll have to double check my code after Mr RBs results.

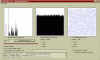
Edit: added the test result from Diehard Battery (blackout.txt) (80 million bits generated and tested).. and with a quick look I think the Black RNG passed all 15 test. I don't know what happened with the histogram I plotted. Have to check that later.

EDIT: I believe the histogram is correct. When I generate 16bit numbers, the histogram is quite uniform from 0 to 65535. But, when I generate 32bit integers the histogram is uniform only from 10000 to 2^32. Everything below 10000 is zero (the best case I was able to generate so far). So, there are some major issues with the Black RNG.

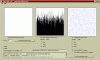
EDIT: More histograms and scatterplots. There seems to bee an obvious structure in the individual 32bit integers in the generator cache. I used 6400 bit cache with the same 17 cylinder engine Mr Black used in his example code. There was 50 passes between each number saved.

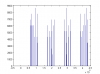
The "Histogram-of-first-32bits.png" shows the distribution of the first 32bits generated (50 passes between each number saved). Very horrible looking distribution for a RNG.

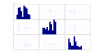
The "ScatterMatrix.png" shows the distribution of random 3-tuples generated.. The "3DscatterPlot.png" shows how the generated 3D points cluster on few spots in the 3D space.

So, my conclusion is, that even if the Black RNG passed the Diehard Battery with good results, the generated numbers still have a very strong structure in them. This structure is well hidden if the cache is very large i.e. million bits. But large cache won't remove the structure, it only interlaces multiple structured sequences together. The setup that Mr RB calls the "the worst case" is:

For the random data I just used the value in the Black RNG "cache", this is a worst case scenario as normally you would generate data on the fly as the engine progresses.

This, in my opinion, is the best case you can get. The whole (million byte) cache should be used as a sequence of random bytes. Then the whole cache should be "scrambled" with some passes with the engine.. and even then I wouldn't trust the data enough to use it in Monte Carlo applications.

I also experimented with different amounts of passes of the cache. Even with 500 passes to the whole cache before saving the next generated number, there was practically no change in the generated pattern. Only thing affecting the pattern is the cache size. And that is equivalent to setting up multiple generators in parallel with different seeds.. effectively leading to different sets of structured sequences. All datasets were generated with the cache first filled with random numbers from a library RNG.

 

[nsaspook]

nsaspook-

Who says an algorithm cannot be infinite? Such closed minded thinking...

The problem is 'infinity' is not actually a number. Your program no matter how clever will repeat the number sequence because a computer only has a finite number of states, the sun might be a cold lump of iron but it will happen.

True RNGs are not algorithmic.

https://www.electro-tech-online.com/custompdfs/2010/11/Onrandom-1.pdf ∞

 

[birdman0_o]

Never heard of Monte Carlo method! Insannne

 

[Mr RB]

To MisterT- Thanks for implementing and testing my RNG. I'd like to comment on your results;

1. A 10+1 cylinder engine (that you used) produces inferior results to the 17+1 engine I used in my most recent tests. Also the quality of the output depends on the values used within the engine, the values used in my last tests worked well.

2. Your 32bit histogram test is flawed, likely your other histograms. 32 bit values have a range of 0 - 4.3billion, so your "<10000" represents just 0.00000233 of the total range! With your small amount of 100000 samples it is quite statistically likely none of those 100000 samples will happen fall within such a tiny slice of the pie. You need to stick to 16bit histogram or less with that sample size.

3. Re the further tests, a 6400 bit cache is too small for really good entropy, as the engine suffle event occurs every 256 bits average, and you are getting too few engine shuffles per sample loop as evidenced by the patternation shown in histograms and scatterplots. That patternation will also be evident if you have not correctly implemented the engine shuffle part of the algorithm, which is the only time I have seen patternation from a large enough cache.

MisterT-

This, in my opinion, is the best case you can get. The whole (million byte) cache should be used as a sequence of random bytes.

Not so, even though the instantaneous cache content is extremely good and can pass the ENT and diehard tests as a good random number itself, it is not the "output" of the RNG. The highest quality entropy is when bits are generated over time, ie one bit per X engine bitswaps. As the engine shuffle occurs after average 256 bitswaps, if X is significantly higher than 256 the entropy is much superior than just testing a chunk of the cache.

I will try to duplicate your results with a known-good RNG over the next couple of days. Your histograms and scatterplots definitely look funky, not like the stuff I have seen.

Nsaspook-

Your program no matter how clever will repeat the number sequence because a computer only has a finite number of states, the sun might be a cold lump of iron but it will happen.

I understand your thinking but you are wrong. Many common math processes produce an output that does not repeat, for instance if you have an algorthm to compute Pi its output will not repeat. There's no reason to believe that an algorithm *must* repeat it's entire output (a global repeat), although over enough time many small repeated sections will be found, as also happens with pure natural random data. Cryptographic RNG algorithms that scramble themselves (like mine) can be free of a global repeat, although global repeat is common in other (linear) RNGs.

Sorry again for posting off topic in this thread. However if someone posts questions or evaluations of my RNG I think it is right to reply. Maybe the moderator can move all the RNG posts to a separate thread?

 

[3v0]

If you wish I can split the tread ?

 

[Mr RB]

That would be wonderful 3V0. The RNG related posts are practically devoid of C/asm discussion and vice versa so splitting into 2 threads sounds like a good idea.

On a RNG note, after examining MisterT's findings and charts above, I took the time to today (between replacing my hot water system that blew up) to code scattergraphs into my own RNG software and updated my histogram code to display 8,16 and 32bit histogram data. I'm not sure what MisterT got wrong wither in his BlackRNG simulation or in his analysis/charting code, but I have done it right in both cases and there are a heap of screenshots on my RNG page of what the generated data, histograms and scattergraphs actually look like.

I have also provided free Windows software so people can generate their own data, and a 1Mb file of good data if people just want to test the random data.

Sample screenshot is below and my RNG page is here; My RNG algorithm page

 

[misterT]

I'm not sure what MisterT got wrong wither in his BlackRNG simulation or in his analysis/charting code, but I have done it right in both cases and there are a heap of screenshots on my RNG page of what the generated data, histograms and scattergraphs actually look like.

Nothing wen't wrong with my scatterplots. The difference is that I was looking for structures in the generated data and you were not. It took me a while to find those structures.

The idea of testing is to find weaknesses in the system. When you find a problem you either fix it or you document it very well so that problems can be avoided.

I did use a small cache to find those structures in the data. I haven't been able to find visible structures in data that is generated with very large cache, but it does not mean there aren't any.. and the structures I found suggest that there might be some in properly generated data also.

 

[nsaspook]

Nsaspook-

I understand your thinking but you are wrong. Many common math processes produce an output that does not repeat, for instance if you have an algorthm to compute Pi its output will not repeat. There's no reason to believe that an algorithm *must* repeat it's entire output (a global repeat), although over enough time many small repeated sections will be found, as also happens with pure natural random data. Cryptographic RNG algorithms that scramble themselves (like mine) can be free of a global repeat, although global repeat is common in other (linear) RNGs.

Not repeating and being secure are different. PI is not a random number and exists as a constant external of any program or algorithm. I should have restricted my comments to a cryptographically secure deterministic random bit generator.

Inherent nonrandomness
Because any PRNG run on a deterministic computer (contrast quantum computer) is necessarily a deterministic algorithm, its output will inevitably have one property that a true random sequence can never have: periodicity. It is certain that, if such a generator has only a finite memory, it will, given sufficient time, revisit a previous internal state, after which it will repeat the prior sequence forever. Non-periodic generators for deterministic computers can be designed, but memory requirements would grow without limit during runs; this is not, of course, possible in real equipment. A PRNG can be started from an arbitrary starting point, using a 'random' seed state; it will always produce the same sequence thereafter when initialized with that state.

**broken link removed**

RANDOM.ORG - Introduction to Randomness and Random Numbers

Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin. .. John Von Neumann (1951)

 

[Mr RB]

(edit)Thank you 3V0 for moving these posts from the other thread! (/edit)

MisterT, I took the time to replicate your test where you said my RNG "failed" generating 32 bit numbers from a small cache.

This was the engine I used;
6400 bit (800 byte) cache
17+1 cylinder engine (standard start values)

Method;
1. start with typical text file as the seed
2. perform 50 loops through the 6400 bit cache
3. make sure engine pos is >100 bits so the first 32 bits must be done
4. save the first 32bits of the cache appended into a file
5. repeat steps 2-5 until 7500 32bit samples were generated

Results;
Total loops through the 6400 bit cache was 375000, ie 50 loops * 7500 generated samples.

The first screenshot below shows the state of the 800 byte cache after such a huge amount of loops, as you can see the histogram and scattergraph appear perfect indicating apporpriate randomness in the cache and no evidence of settling into patterns after 375000 loops. The spectral distribution of the cache (and 0-9 range) is exactly what I would expect to see from 800 random byte samples with a 3.125 samples/bar mean.

Now the 7500 32bit generated samples (file size 30000 bytes) was tested using John Walker's ENT.exe program, the result is shown in the second image. The arithmetic mean, Monte Carlo Pi and Serial correlation are all good for a 30000 byte sample and the important Chi Squared value that would easily indicate any patternation (as MisterT reported) showed no patternation with a great result of 29.15%, all results not too far from a radioactive decay RNG result.

The 30000 byte file of the generated data "test32.ENT" is attached.

Finally I modified my Windows program to load and display the test32.ENT file. This is shown in the 3rd screenshot. The spectral histogram of 32bit numbers is exactly as expected for good random data in a sample size of 7500, with a range of 13-46 and mean of 29.29. Likewise the scattergraph with 3750 32bit XY points plotted, is as random as it gets.

Last picture is the histogram that MisterT claimed was produced by the same tests, which is nothing like the real results. If anyone wants to see any of my source code to replicate these tests just ask.

This test of extracting the first 32 cache bits after every 50 loops through a small cache is NOT the way I would generate random data. For this amount of data over time it would be far better to generate 1 output bit for every 1.56 passes through the cache maximising the number of engine shuffles and scrambling between each bit generation. However even with such a difficult test the RNG holds up well.

MisterT, I no longer have any confidence in your ability to code up a working version of the Black RNG and test its data. Even your test itself is not representative of a logical way to generate data from my RNG.

 

[misterT]

Finally I modified my Windows program to load and display the test32.ENT file. This is shown in the 3rd screenshot. The spectral histogram of 32bit numbers is exactly as expected for good random data in a sample size of 7500, with a range of 13-46 and mean of 29.29. Likewise the scattergraph with 3750 32bit XY points plotted, is as random as it gets.

It is weird that sample size of 7500 can fill up histogram like that when the number of the values range from 0 to 2^32. Can you make a histogram that also shows the values of the axes? What is the bin size of the histogram? How tall are the columns of the histogram? What do you mean by "range of 13-46"?

 

[Mr RB]

Nsaspook-

Not repeating and being secure are different. PI is not a random number and exists as a constant external of any program or algorithm. I should have restricted my comments to a cryptographically secure deterministic random bit generator.

That's a good point. But my point is that if algorithmic processes can produce output that has no global repeat, and cryptographic algorithms can produce acceptable random short term data, there is no reason why the two systems cannot be merged into a larger more complex system that maintains the key features of each system, ie; no global repeat and random short term output data.

The result is that you have shifted the "repeating" into small variable-sized bitstrings, which are repeated randomly, with no global repeat. If those bitstrings are short enough you have the same output as generated by a pure natural entropy source, which consists of a huge number of small identifiable repeating bitstrings in random order.

My RNG will produce the same cache sequence of events whenever it starts from the same state.
The math for calculating the number of states is (I think this is right);
number of permutations of cylinder setup; for 18 cyls = 1*2*3*4*5*6*7*8*9*10*11*12*13*14*15*16*17*18 = 96.035 * 10^15 (I think) times
number of perms of held bit; 2 times
number of perms of cache; 2^cache size = 2^8000000 divided by
cache size (as state can occur on any cache bit) = 8000000

So that is;
96.036*10^15 * 2 * 2^8000000 / 8000000

So there is no guarantee that any short or medium string of numbers will have a global repeat, although a chance of global repeat gets more statistically likely over a log enough time.

However I stated before that the cache istself is not the output of the random number generator, just a seed with very good entropy. The output should be generated over time by extracting bits from the RNG over time. If any real world event (like your PC's clock PIT chip interrupt which has its own xtal) is used to extract a bit from the RNG at that point in time the output will be a pure naturally random bit stream because of the high entropy of the cache after any significant period of time means it will be unknown what bit will be extracted at that instant.

On the other hand you could algorithmically extract one bit after every N engine shuffles or every N bits processed, with N being sufficiently high so that any global repeat is distributed though a much smaller number of bits randomly extracted throughout the global repeat. This would probably be slower than just adding a real world stimulus (like above) but should be able to produce very large data streams from algorithm alone.

And if you just need small quantities of good entropy (up to a few megabytes) just pull data direct from the RNG cache.

Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin. .. John Von Neumann (1951)

With all respect to John Von Neumann and his contributions to computing, he said that at the dawn of the computing age with 4bit computers that worked at low kHz speed with very small program sizes. I have a feeling that with his brain in modern times, where even desktop PCs are 64bit at >2GHz and Gbytes of ram, he may have said something quite different...

 

[Mr RB]

MisterT-

There is no way a sample size of 7500 can fill up a histogram like that when the number of the values range from 0 to 2^32. Can you make a histogram that also shows the values of the axes? What do you mean by "range of 13-46"?

The spectral distribution histogram in my screenshots shows all the samples plotted on a bar chart.

The chart is 256 pixels wide (for convenience) so there are 256 vertical bars, and each bar shows how many of the samples fall within that 1/256th of the total possible range. As they are 32bit samples being charted the total range is 0 to 4.3billion (same linear range as shown in your histogram).

Tha value of the axes is just scaled for good viewing, as stated by the range of min-max bar height (13-46) the tallest bar indicates 46 samples are in that bar.

 

[misterT]

MisterT, I took the time to replicate your test where you said my RNG "failed" generating 32 bit numbers from a small cache.

This was the engine I used;
6400 bit (800 byte) cache
17+1 cylinder engine (standard start values)

Method;
1. start with typical text file as the seed
2. perform 50 loops through the 6400 bit cache
3. make sure engine pos is >100 bits so the first 32 bits must be done
4. save the first 32bits of the cache appended into a file
5. repeat steps 2-5 until 7500 32bit samples were generated

Total loops through the 6400 bit cache was 375000, ie 50 loops * 7500 generated samples.

Finally I modified my Windows program to load and display the test32.ENT file. This is shown in the 3rd screenshot. The spectral histogram of 32bit numbers is exactly as expected for good random data in a sample size of 7500, with a range of 13-46 and mean of 29.29. Likewise the scattergraph with 3750 32bit XY points plotted, is as random as it gets.

That is quite useful result you created. It got me wondering: How fast the data converges into the pattern? I initialized my cache with random data from a library RNG routine. It would be interesting to know how the data got stuck into fixed pattern.

This is the setup:

230*32 bit cache.
17+1 cylinder engine (standard start values).

1. start with random numbers from (available) library function as the seed
2. perform 50 loops through the 230*32 bit cache
3. save the first 32bits of the cache appended into a file
4. repeat steps 2-4 until 100000 32bit samples were generated

And attached is the plot of generated data. Horizontal axis is the (running) number of data and vertical axis is the (random) data value.

My quick observation is: The bigger the cache, the longer it takes the data to start repeating itself. And the transition is amazingly sharp.

So, could you (Mr RB) repeat your test with at least 100 000 samples? I noticed that with cache of 240*32 bits I didn't get any structure with 100 000 samples. And, with 200*32 bits of cache, the data started repeating itself quite early.

UPDATE: There is more to it.. With 229*32 bit cache, the 100 000 samples seemed to be uniformly distributed, but with 230*32 cache, the data is like the one plotted in the attached figure.

UPDATE: My library RNG took its seed from the system clock. I changed that to a constant so I get the same initial value for every cache.. Turns out the initial cache value is a big factor in how fast the data starts to repeat itself. I couldn't repeat the results in the attached plot with different initial cache. The results vary from better to worse.

UPDATE: The structure seems to have a very clear self-similar pattern (Cantor set -type). Black RNG could be more of a fractal engine than a random number generator. I had fun zooming into the pattern with Matlab. I'll try to make some good images to illustrate this self-similarity.
https://en.wikipedia.org/wiki/Cantor_set

 

[nsaspook]

Nsaspook-

That's a good point. But my point is that if algorithmic processes can produce output that has no global repeat, and cryptographic algorithms can produce acceptable random short term data, there is no reason why the two systems cannot be merged into a larger more complex system that maintains the key features of each system, ie; no global repeat and random short term output data.

The result is that you have shifted the "repeating" into small variable-sized bitstrings, which are repeated randomly, with no global repeat. If those bitstrings are short enough you have the same output as generated by a pure natural entropy source, which consists of a huge number of small identifiable repeating bitstrings in random order.

I don't see it as much different from just using a part of the PI number sequence as the non-repeating component. As long as nobody knew it was PI it would appear random.

With all respect to John Von Neumann and his contributions to computing, he said that at the dawn of the computing age with 4bit computers that worked at low kHz speed with very small program sizes. I have a feeling that with his brain in modern times, where even desktop PCs are 64bit at >2GHz and Gbytes of ram, he may have said something quite different...

Computer power works both ways, the lack of pure hardware power caused people to be very percise about programming logic and proofs for crypto machines.

KW-37 - Wikipedia, the free encyclopedia Designed in the 1950s, used until the 1990s.

Simple PIC timer based PRNG. https://www.electro-tech-online.com/custompdfs/2010/11/emnets.pdf

Hardware TRNG. https://www.electro-tech-online.com/custompdfs/2010/11/quantis-whitepaper.pdf

 

[Mr RB]

MisterT-

230*32 bit cache.
17+1 cylinder engine (standard start values).

1. start with random numbers from (available) library function as the seed
2. perform 50 loops through the 230*32 bit cache
3. save the first 32bits of the cache appended into a file
4. repeat steps 2-4 until 100000 32bit samples were generated

MisterT- I simply can't get the RNG to settle out in the way you describe in your test after 100000 * 50 loops.
Please produce your starting seed value so I can actually run it and then say if your test is correct or if there is a flaw in your method!

I can hypothesise that this effect may be possible. If using a small enough cache, that happens to be a size synchronous to 32bits, (ie cache size = X*32) that you may be able to get a 32bit pattern to occur after a very high number of iterations. Also, a seed that contains mathematically repeating patterns like that generated by a crude RNG (which may also be 32bit patterns) is the worst case scenario as it can encourage patterns to develop in this RNG.

As you reduce the cache size of a self scrambling RNG you reduce it's ability to produce entropy until you eventually get below a critical point where it can no longer produce enough entropy to maintain its integrity. Likewise if you maximise other negative factors like choosing a cache size of X*32 plotted against 32bit results. I'm sure I could reduce the cache size far enough, and feed in just the right starting seed, to get it to fail quite quickly.

But just because it is possible to reduce an RNGs integrity below the ciritcal point, to finally get it to fail is no proof that it would have ever failed if its integrity had not been compromised. As an example if I reduce the cache size to 10 bits it would generate patterns from the very first iteration.

If you *must* use a very small cache and still wanted good long term entropy I would increase the number of cylinders a lot, use a 6 or 7 bit mask to increase the frequency of engine shufles, and use a prime number for the cache size. But of course if you want top quality entropy then use the RNG with large values as recommended.

 

[Mr RB]

Nsaspook-

I don't see it as much different from just using a part of the PI number sequence as the non-repeating component. As long as nobody knew it was PI it would appear random.

Imagine something like this;
1. use a Pi algorithm to generate the next set of 20 digits, guaranteed free of global repeating.
2. merge the 20 Pi digits thoughout the 8000000 bit cache of my RNG so they replace about 10% of the cache, causing partial re-seeding.
3. run the RNG though 20 loops, generating high entropy data
4. use that high entropy data to self-extract a variable sized bitstream of 50 to 1000 bits, (this is the output of the entire process).
5. repeat...

So between us we've devised a way to generate crypographically secure entropy guaranteed free of global repeat.

Nsaspook re Von Neumann-

Computer power works both ways, the lack of pure hardware power caused people to be very percise about programming logic and proofs for crypto machines.

I wonder what Von Neumann's quote would have been if he had been asked about simulating real chaos weather patterns on his computer? Probably the same...

Every age of man has seen Universities teaching theories that were later proven to be wrong, as technology and knowlege progressed. Dare to think "HOW can I do it" rather than "I was taught it can't be done".

 

[ericgibbs]

hi Roman,
I have always been taught that in the real world there is no such animal as a 'true' random number.

Assuming integers from zero thru to infinity is the absolute SET of numbers from which a 'selection' can be made, this means that only numbers 'selected' from that absolute SET is truly random.

However big you make your real world 'computed' SUB SET you are not generating random numbers, you are making random 'selections' of numbers within that SUB SET.

Regards

 

[misterT]

MisterT-

MisterT- I simply can't get the RNG to settle out in the way you describe in your test after 100000 * 50 loops.
Please produce your starting seed value so I can actually run it and then say if your test is correct or if there is a flaw in your method!

Try all zeros as a seed and a mask "01011001" for engine shuffles. Cache 200*32.. try also cache 210*32. Otherwise the same setup as before. The algorithm recovers very nicely from the bad seed. After about 25000 iterations the first 32 bits in the cache start repeating a pattern. The result look similar to what I got with random seed.

I'll clean up and comment my code so you can take a look at that also. There is always a chance of bug in the code.

EDIT: I just noticed that your implementation of the engine is different from your illustrations. In the illustrations you first toggle the bit and then exchange the next bit.. and the next position is calculated relative to the first bit that was modified. This is how I implemented my Black RNG. But, in your code, you first exchange the bit and then toggle the next bit.. and the next position is calculated relative to the second bit modified. Also the shuffling of the engine is in different stage in the illustrations and your implementation. Also, your implementation makes every engine "cylinder" value effectively one larger, because you first move one bit forward to toggle a bit and after that you move forward by the number in the next cylinder.

 

[Mr RB]

Ericgibbs-

However big you make your real world 'computed' SUB SET you are not generating random numbers, you are making random 'selections' of numbers within that SUB SET.

I guess that is right, which means of course that you can't "generate" a number of any type, at all... You can only "select" numbers that already existed in the universe. However I'm not sure how that helps at all.

MisterT- I'll try your seed and mask value tomorrow.

Yes the final version of the RNG as it stands does the transposition of the bit at X and the toggling of the bit at X+1. This produced far better entropy in early testing than the other way around and I have used it since... I apologise for the diagrams not being updated, I will fix that up. It also explains something about the weird results you have been getting.

But the shuffling is shown correctly in the diagram I believe, as the cylinder value is shuffled directly before that cylinder is used for the next forward move event. This reduces latency between mask detected and when it causes an effect on the cache. I'm open to suggestions of a better way to draw it, but I think that is right as it shows the cylinder swap to the right, which is the cylinder that will be used to control the next move.

Also, your implementation makes every engine "cylinder" value effectively one larger, because you first move one bit forward to toggle a bit and after that you move forward by the number in the next cylinder.

No that is not correct, a temporary variable "next_pos" is created and used to index and toggle the following bit, but that does not affect the main index variable "pos" which is used for all movement.

If you had implemented it as you say, it would compromise the RNG terribly as it would no longer be able to move forward 1 bit, as the minimum move value becomes 2 which is nasty for RNGs and particularly this one as it modifies 2 bits at a time!!

Can any math experts please comment on my rough calcs for the number of possible engine states (post #31), particularly the cylinder permutations calc (for 18 cylinders) and the /8000000 concept. I've been thinking the /8000000 is not valid as any "state" must be instantaneous, not existing at all indexes within the cache. As the cache is circular, there is only one index (where it is now).

 

[misterT]

No that is not correct, a temporary variable "next_pos" is created and used to index and toggle the following bit, but that does not affect the main index variable "pos" which is used for all movement.

If you had implemented it as you say, it would compromise the RNG terribly as it would no longer be able to move forward 1 bit, as the minimum move value becomes 2 which is nasty for RNGs and particularly this one as it modifies 2 bits at a time!!

I have implemented the engine as in your illustrations. I missed that you had a temporary variable for the next bit, so no problem there. That part is also correct in my code. I can change my code to reflect yours i.e. change the order of bit toggles and exchanges.

Can any math experts please comment on my rough calcs for the number of possible engine states (post #31), particularly the cylinder permutations calc (for 18 cylinders) and the /8000000 concept. I've been thinking the /8000000 is not valid as any "state" must be instantaneous, not existing at all indexes within the cache. As the cache is circular, there is only one index (where it is now).

If you use 17 cylinders and the possible cylinder values are the 18 numbers: {1,2,3,1,2,3,4,5,7,1,2,3,6,4,1,3,11,9}

Number of unique cylinder permutations is:

18! / (4! * 3! * 4! * 2!) = 926 269 344 000

You must divide by the factorials because you have number 1 four times in the possible values, number 2 three times etc. If all the numbers in the engine were unique, the number of permutations would be 18! / (18-17)!. In general, if you choose k cylinders from n unique numbers, the number of permutations is n! / (n-k)!.

You cannot include the pointer position in the calculations, because moving the pointer is the same as moving the values in the cylinders or in the cache (which is same as getting another permutation of cylinders or cache, and we already included all of them). So the /8000000 concept is wrong. Other than that your calculation was almost correct.

If you have a million bit cache, you have 926 269 344 000 * 2^1000000 * 2^8 unique states. The last 2^8 comes from the exchanged bit history. And after each state the sequence of random numbers is always the same. So, if one state comes up twice, the generated numbers (states) start repeating.

If we choose any state at random, the odds of any state to come up is

P = 1 / (926 269 344 000 * 2^1000000 * 2^8)

The odds that the same state comes up exactly K times after picking N states at random is:

P_(K, N) = P^K * (1-P)^(N-K) * ( N! / (K! * (N-K!)) )

To get the odds that the same state comes up at least 2 times, we need to calculate:

P_(2, N) + P_(3, N) + P_(4, N) + ... + P_(N, N)

Which is the same as calculating
1 - P_(0, N) + P_(1, N)

Which in turn becomes:
1 - (1-P)^N + N * P * (1-P)^(N-1)

Above calculations assume that each state is equally possible and independent.

Of course, the states are not independent in the Black RNG. Black RNG defines an ordered set of states (like basically all RNG algorithms do). The maximum period you can theoretically get is the number of unique states, but the odds of this happening is very small. And, at the end, the period of the generator has little to do with its quality.